
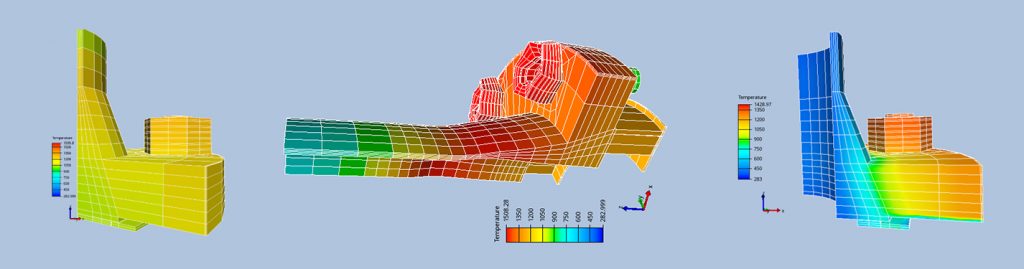
Flanges exposed to fire
Flange analysis is performed by use of Brilliant, Petrell’s proprietary numerical simulation platform. Brilliant is fully integrated CFD (Computational Fluid Dynamics) system and Finite Element Method (FEM) system. It includes a library for material properties of a number of metallic materials including insulation materials, and also a comprehensive thermodynamic library (ThermoProp).
Brilliant is tailored-made to serve multi-physic simulations, and it is used a platform for other applications including VessFire, Brilliant NWS (Near Wellbore Simulator) and SolidCO2Sim.
Brilliant is built on fundamental conservation equations for transport of continuum properties as:
• Momentum equation (Newton’s second law F=ma)
• Mass continuity
• Energy equation
• Transport of species
• Chemical reactions
Numerical Models
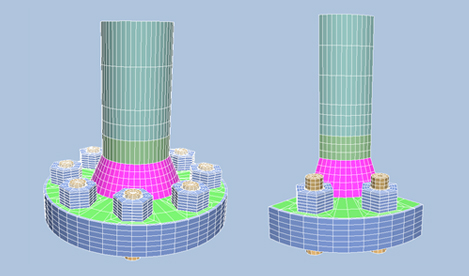
Numerical models have been developed for ASME RF (Raced Face), RJT (Ring Joint Type), Compact and Hub flanges, and different materials in flange, gasket and bolts/nuts have been implemented (Figure 1, Figure 2, Figure 3).
Geometrically, the flanges are symmetric and the boundary conditions for the symmetry planes are easy to implement. The model system is flexible and can be adapted to a ¼ of a half flange, a half flange and even the whole flange. A quarter of the flange is used for the calculations to save simulation time.
All simulations are generated by running a script that catches required parameters from relevant ASME standards.
A condition for applying a reduced model is that the heating is uniform around the flange, which is different from experiments. To see the effect of non-uniform heating, a full 360˚ model should be run.
Uniform heat load
Higher temperature leads to reduction of the strength of the steel, and consequently a reduction in the ability to take forces. When comparing with experiments, it makes sense to use temperature variation as seen in the experiments, but in calculations performed for design purpose, it makes no sense to apply variation in temperature as part of the scenario. Because a real fire has no general load profile, the scenario description for design purpose should assume a uniform heat load. It is therefore interesting to see how close a uniform heat load comes to the results of an experiment. In a non-uniform heat load situation, the weakest part of the flange might start a chain reaction that leads to rupture as a consequence of force transfer between bolts. The weakest part of the flange is the one with the highest temperature and the lowest strength, therefore the highest temperature for all bolts describes the situation where the flange is at its weakest. Applying the highest temperature as the case temperature make the calculations staying on the conservative side.
The pretension force in the bolt is created by giving an initial displacement on the bottom side of the bolt.


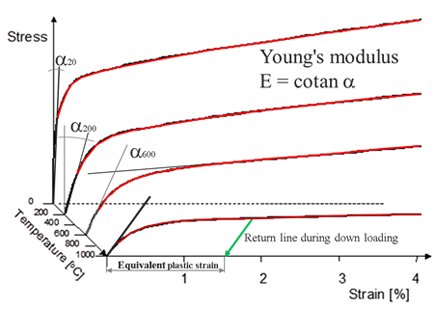
The material properties required in a Finite Element simulation are, in addition to the yield stress, Young’s modulus and data for plasto-elastic nonlinear behaviour (hardening), Poisson coefficient, thermal linear expansion, specific heat, conductivity and density. Most of these are dependent on temperature, but few properties are available for temperatures above 400°C. The temperatures of interest for our calculations are above 400°C and especially in the range above 1000°C.
Plastic domain
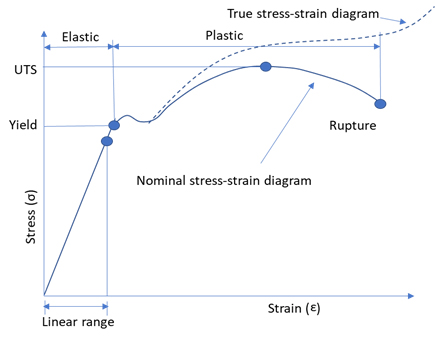
Young’s modulus describes the linear part of the relation between stress and strain. The linear domain is elastic. That means a point returns to its original position with unloading. When the load exceeds the yield stress, the material enters the non-linear domain, also called the plastic domain. The material in the plastic domain will get a permanent deformation and a point will not return to its original position with unloading. The material will return along an elastic path, but from a permanent deformed position. In the plastic domain the material goes through a process called hardening, the material becomes stronger caused by the permanent deformation. Figure 4 shows stress-strain curves for true stress and engineering stress (called normal stress in the figure) and Figure 5 shows the stress-strain relation during the linear (elastic) and non-linear (plastic) domain as temperature changes. Two effects on the Young’s modulus can be seen. Increase of temperature shorten the length of the elastic domain and the Young’s modulus is also reduced.
The flange models allow for determination of time to leak and leak rate.


